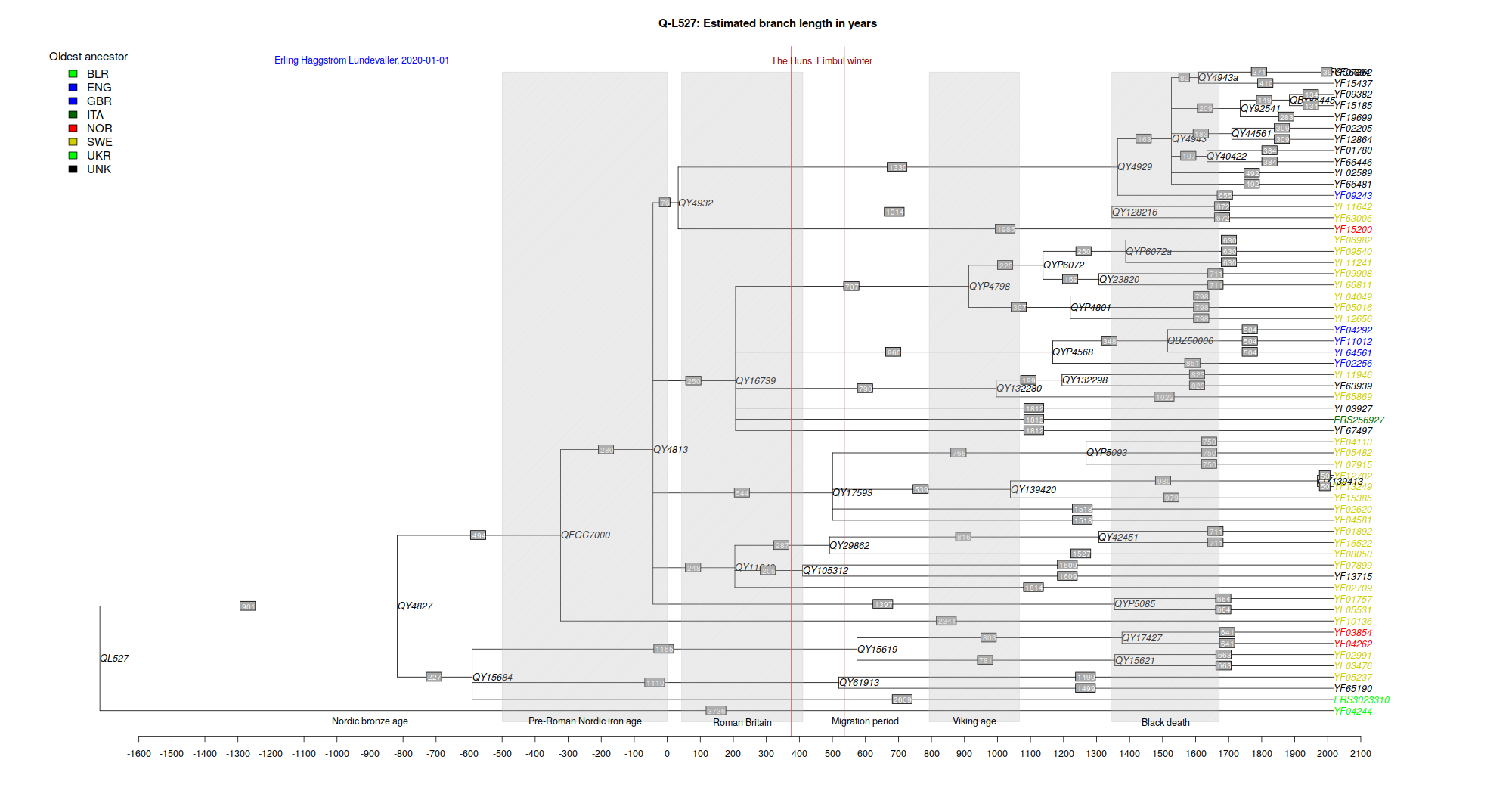
This is the current status of the family tree of Q-L527 based on the data at YFull (Updated 2020-01-01). Two interesting kits from Belarus and Ukraine on old branches. They might give an indication of a possible migration route to Scandinavia. The main expansion in number of branches of Q-L527 seems to be before the viking age. I have estimated branch length in years with the Ape package in R using maximum likelihood and the “strikt model”. The idea is to calculate the most likely branch length given the number of SNPs on each segment. It is assumed that the rate that governs the random mutations are constant. This is a standard way of estimating branch splits and TMRCA (Time to Most Recent Common Ancestor).
The rightmost codes refer to actuall test persons (YFxxxxx). Notice that this way of dating puts less weight on the Belarus sample compared to Yfulls estimate, pushing the origin of Q-L527 back in time. This is because the Belarus had fewer SNPs and Yfulls method weight this sample very high. Yfulls eatimate of the age of Q-L527 is 3680 years if the Belarus kit is not included. If it is included: (3680+2297)/2 = 2988 ybp. This is of course to put to much weight on this kit.
YFulls version of the tree can be found at: https://www.yfull.com/tree/Q-L527/.
The number of SNPs used for the estimation can be seen in the figure below:
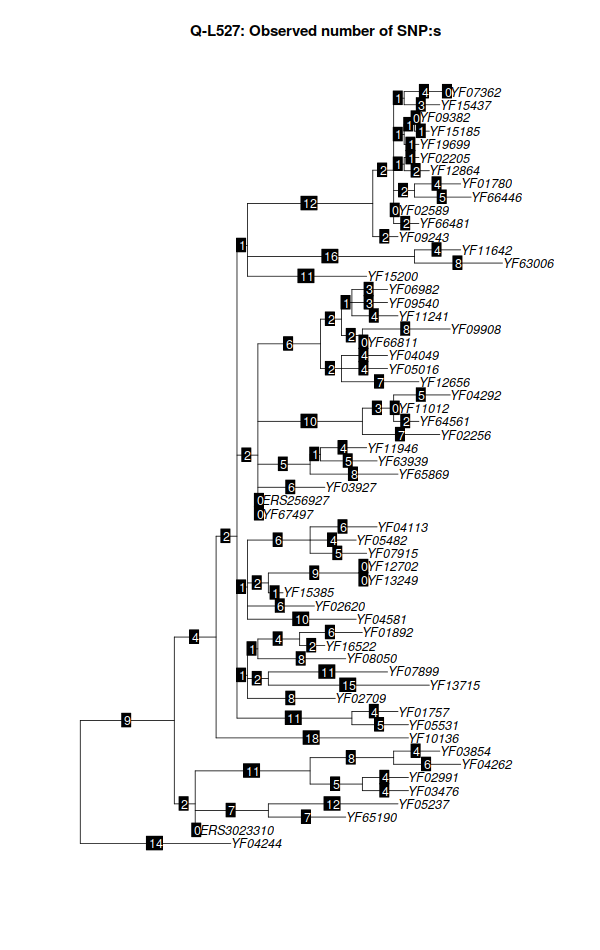
The idea of maximum likelihood here is to choose the branch lengh that gives the most likely “pedigree” given the observed number of SNPs at every branch. The mean time to a new SNP is assumed to be 144.41 years, constant over all branches. (If this assumption hold it means that other methods of calculating TMRCA, such as YFulls own is less likely to be true than this method). This makes also the strikt model suiatable. Some background for these choises can be found in:
Tagankin, Vladimir, and Vadim Urasin. “Defining a New Rate Constant for Y-Chromosome SNPs based on Full Sequencing Data.”
Brown, Richard P., and Ziheng Yang. “Rate variation and estimation of divergence times using strict and relaxed clocks.” BMC Evolutionary Biology 11.1 (2011): 271.